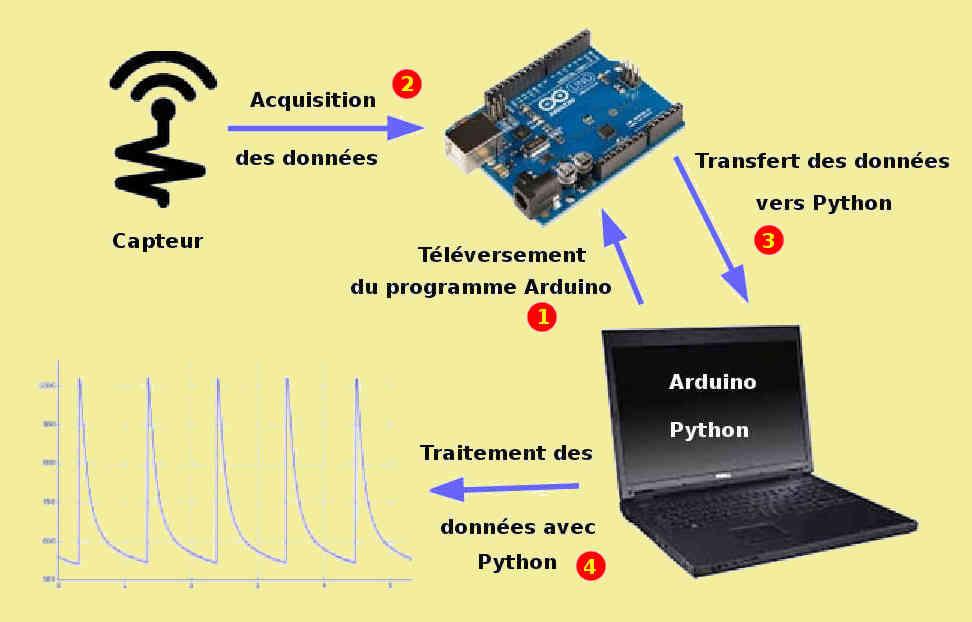
8. Introduction au traitement du signal▲
8-1. Un signal c'est quoi ?▲
Dans le cadre de cette formation, nous utiliserons la définition d'un signal comme la représentation physique d'une information à transmettre ou de façon équivalente comme une entité qui sert à véhiculer une information.
Attention, toute grandeur physique qui varie au cours du temps n'est pas un signal. En effet, les signaux sont tout le temps « bruité ». Le « bruit » est l'ensemble des phénomènes perturbateurs qui gênent, voire empêchent la perception ou l'interprétation de l'information suivant le rapport Signal sur Bruit. La grandeur physique véhiculant le signal doit être mesurable et pourvue d'une unité. Les grandeurs électriques sont souvent utilisées comme signaux transportant l'information. Mais on trouve aussi fréquemment des signaux lumineux, sonores ou radio.
Cette définition du signal amène à associer la grandeur physique véhiculant le signal à sa description mathématique sous la forme d'une fonction du temps.
8-2. Continuité et discontinuité en temps▲
Un signal peut-être représenté par une fonction qui varie dans le temps notée kitxmlcodeinlinelatexdvpf : t \mapsto y(t)finkitxmlcodeinlinelatexdvp, on peut distinguer plusieurs cas possibles suivant les valeurs prises par la variable kitxmlcodeinlinelatexdvptfinkitxmlcodeinlinelatexdvp :
- les signaux à temps continus, les valeurs kitxmlcodeinlinelatexdvpf(t)finkitxmlcodeinlinelatexdvp sont définies pour kitxmlcodeinlinelatexdvpt \in \mathbb{R}^+finkitxmlcodeinlinelatexdvp. Par convention, on suppose que la variable temps ne peut pas prendre de valeurs négatives ;
- les signaux à temps discret, les valeurs kitxmlcodeinlinelatexdvpf(t)finkitxmlcodeinlinelatexdvp n'existent que pour des valeurs discrètes de kitxmlcodeinlinelatexdvptfinkitxmlcodeinlinelatexdvp, lors d'une acquisition les valeurs de kitxmlcodeinlinelatexdvptfinkitxmlcodeinlinelatexdvp sont prises à intervalle constant.
On distingue également les signaux non quantifiés pour lesquels kitxmlcodeinlinelatexdvpffinkitxmlcodeinlinelatexdvp peut prendre n'importe quelle valeur dans un intervalle continu et les signaux quantifiés pour lesquels kitxmlcodeinlinelatexdvpffinkitxmlcodeinlinelatexdvp ne peut prendre que des valeurs discrètes. Dans le premier cas, on parle parfois de signaux analogiques et dans le deuxième cas on parle parfois de signaux numériques. Attention de ne pas généraliser, les signaux analogiques et numériques sont des sous-ensembles respectifs des signaux continus et discrets.
Remarques : si les signaux continus peuvent être modélisés par des fonctions mathématiques plus ou moins complexes, il n'en est pas de même avec les signaux discrets. Il est plus facile de les définir à l'aide d'une suite de valeurs notée kitxmlcodeinlinelatexdvp(y_i)_{i\in \mathbb{N}}finkitxmlcodeinlinelatexdvp où les kitxmlcodeinlinelatexdvpy_ifinkitxmlcodeinlinelatexdvp représentent les kitxmlcodeinlinelatexdvpf(t_i)finkitxmlcodeinlinelatexdvp. Cette suite de valeurs est aussi souvent appelée échantillons en physique-chimie.
Une autre différence importante à faire pour le traitement du signal est celle qui permet de distinguer les signaux déterministes des signaux stochastiques. Pour le premier, on peut grâce à une étude mathématique prévoir les valeurs qui vont être prises par le signal dans le temps alors que pour le second la valeur à l'instant kitxmlcodeinlinelatexdvpt_ifinkitxmlcodeinlinelatexdvp ne nous renseigne pas sur la valeur à un instant kitxmlcodeinlinelatexdvpt_{i+1}finkitxmlcodeinlinelatexdvp
8-2-1. Dérivée discrète▲
D'après un document de Jean-Luc Charles, enseignant chercheur à l'ENSAM
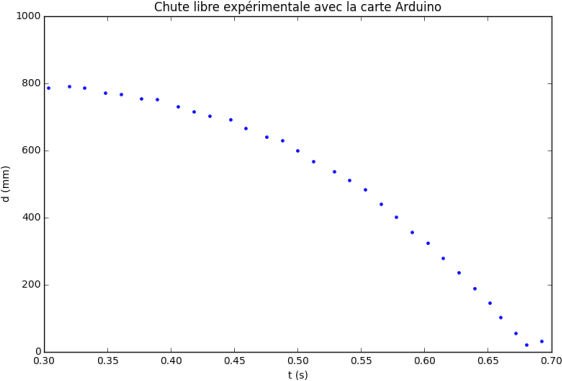
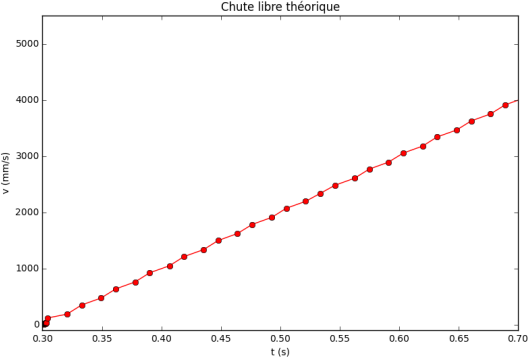
Reprenons les résultats expérimentaux obtenus lors de la chute libre d'un point matériel M sans vitesse initiale. Nous avons fait l'acquisition des positions d'un point matériel de masse m en fonction du temps. Ces valeurs permettent également de tracer le graphique d'évolution des énergies (cinétique, potentielle et mécanique) lors d'une chute libre en calculant, entre autres, la vitesse instantanée en différents points de la chute.
La suite de ce document porte sur la difficulté d'obtenir un calcul acceptable pour la valeur de la vitesse instantanée. Ce qui revient à s'interroger sur le calcul de la dérivée d'une suite discrète de valeurs au cours du temps.
Soit un point matériel kitxmlcodeinlinelatexdvpMfinkitxmlcodeinlinelatexdvp de masse kitxmlcodeinlinelatexdvpmfinkitxmlcodeinlinelatexdvp en chute libre.
On note kitxmlcodeinlinelatexdvp(z_i)_{i\in \mathbb{N}}finkitxmlcodeinlinelatexdvp la suite de valeurs permettant de repérer l'altitude du point kitxmlcodeinlinelatexdvpMfinkitxmlcodeinlinelatexdvp au cours du temps. kitxmlcodeinlinelatexdvpz_ifinkitxmlcodeinlinelatexdvp est l'altitude du point kitxmlcodeinlinelatexdvpMfinkitxmlcodeinlinelatexdvp à un instant kitxmlcodeinlinelatexdvpt_i \ge 0finkitxmlcodeinlinelatexdvp.
On note kitxmlcodeinlinelatexdvp(z'_i)_{i\in \mathbb{N}}finkitxmlcodeinlinelatexdvp la suite des valeurs de la vitesse du point matériel kitxmlcodeinlinelatexdvpMfinkitxmlcodeinlinelatexdvp au cours du temps. kitxmlcodeinlinelatexdvpz'_ifinkitxmlcodeinlinelatexdvp est la vitesse de M à un instant kitxmlcodeinlinelatexdvpt_i \ge 0finkitxmlcodeinlinelatexdvp.
Le calcul de la vitesse du point kitxmlcodeinlinelatexdvpMfinkitxmlcodeinlinelatexdvp à un instant kitxmlcodeinlinelatexdvpt_i \ge 0finkitxmlcodeinlinelatexdvp, encore appelé dans ce cas dérivée discrète à l'instant kitxmlcodeinlinelatexdvpt_i \ge 0finkitxmlcodeinlinelatexdvp, peut se définir de différentes manières :
- dérivée à gauche : kitxmlcodeinlinelatexdvpz'_i = \frac{z_i-z_{i-1}}{t_i-t_{i-1}}finkitxmlcodeinlinelatexdvp ;
- dérivée centrée : kitxmlcodeinlinelatexdvpz'_i = \frac{z_{i+1}-z_{i-1}}{t_{i+1}-t_{i-1}}finkitxmlcodeinlinelatexdvp ;
- dérivée à droite : kitxmlcodeinlinelatexdvpz'_i = \frac{z_{i+1}-z_i}{t_{i+1}-t_i}finkitxmlcodeinlinelatexdvp.
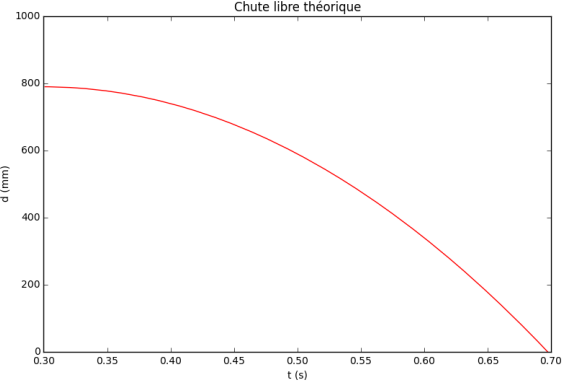
La loi horaire de la chute libre est donnée par : kitxmlcodeinlinelatexdvpz(t) = h-\frac{1}{2}gt^2finkitxmlcodeinlinelatexdvp
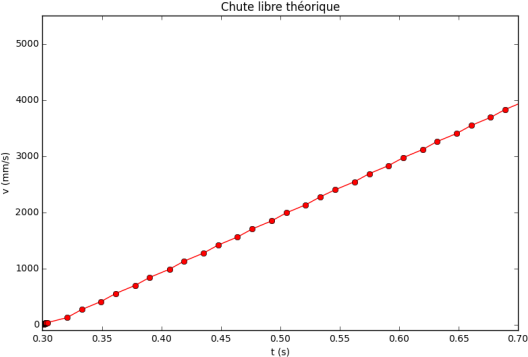
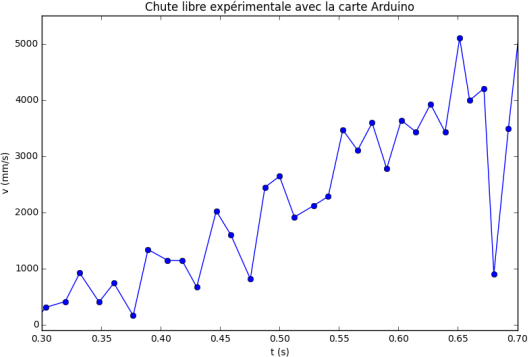
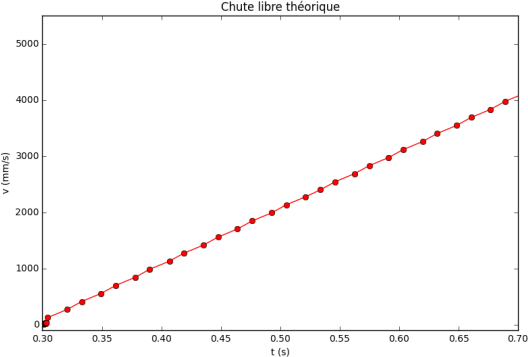
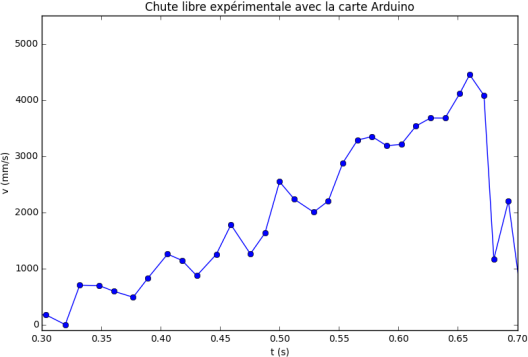
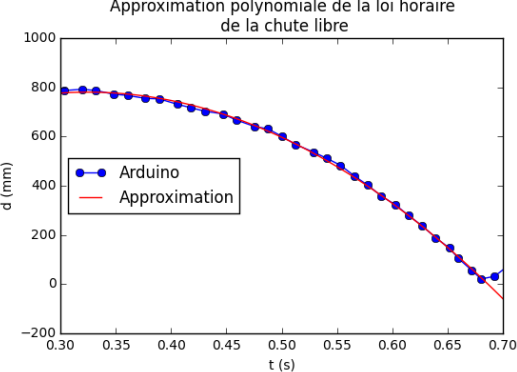
Les graphiques de la loi horaire de la chute libre, expérimentale et théorique, sont les suivants :
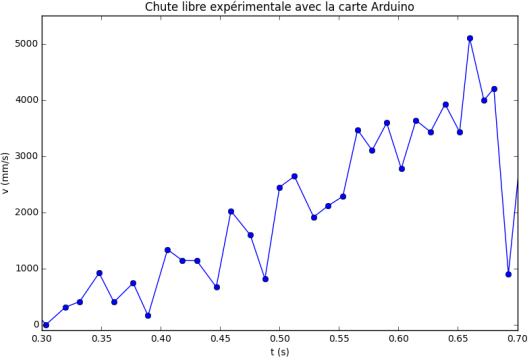
Maintenant, nous allons calculer les vitesses du point matériel M en utilisant les trois relations (gauche, droite et centrée) avec les positions expérimentales et théoriques.
Gauche
Droite
Centrée
On observe que les résultats obtenus pour les calculs de la vitesse instantanée ne sont pas satisfaisants.
8-2-2. Calcul de la dérivée par approximation polynomiale▲
L'idée ici est de faire une approximation polynomiale de la suite kitxmlcodeinlinelatexdvp(z_i)_{i\in \mathbb{N}}finkitxmlcodeinlinelatexdvp par une fonction kitxmlcodeinlinelatexdvpZ : t \mapsto Z(t)finkitxmlcodeinlinelatexdvp sur l'intervalle de temps kitxmlcodeinlinelatexdvp[t_0, t_0+T]finkitxmlcodeinlinelatexdvp avec kitxmlcodeinlinelatexdvpT \in \mathbb{R}^+finkitxmlcodeinlinelatexdvp. kitxmlcodeinlinelatexdvpt_0finkitxmlcodeinlinelatexdvp représente le temps initial et l’on cherche une approximation polynomiale du mouvement pour kitxmlcodeinlinelatexdvpt \in [t_0,t_0+T]finkitxmlcodeinlinelatexdvp. La dérivée de cette fonction notée kitxmlcodeinlinelatexdvpZ'finkitxmlcodeinlinelatexdvp s'obtient alors par simple dérivation du polynôme obtenu.
|
Approximation polynomiale kitxmlcodeinlinelatexdvpZ : t \mapsto -5961t^2 + 3871t + 151.7finkitxmlcodeinlinelatexdvp |
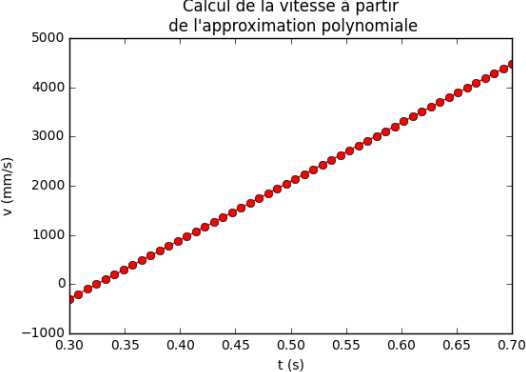
Représentation graphique de kitxmlcodeinlinelatexdvp|Z'|finkitxmlcodeinlinelatexdvp |
Pour calculer l'approximation polynomiale des points de la suite, kitxmlcodeinlinelatexdvp(z_i)_{i \in \mathbb{N}}finkitxmlcodeinlinelatexdvp on utilise la fonction polyfit du module numpy. La fonction polyfit retourne les coefficients du polynôme représentant la fonction kitxmlcodeinlinelatexdvpZfinkitxmlcodeinlinelatexdvp, coefficients qui peuvent ensuite être utilisés avec numpy.poly1d. Puis on trace la vitesse en dérivant la fonction kitxmlcodeinlinelatexdvpZfinkitxmlcodeinlinelatexdvp obtenue.
Pour cela, on utilise les fonctions polyfit et poly1d du module numpy. La première renvoie l'ensemble des coefficients du polynôme, de degré 2 dans l'exemple, ajusté par la méthode des moindres carrés, la deuxième permet de construire la fonction mathématique et la fonction Python correspondantes. Dans l'exemple suivant, je n'ai conservé que les points intéressants de l'acquisition, c'est-à-dire ceux de l'intervalle : [45:75] des listes x et y.
2.
3.
import numpy as np
z = np.polyfit(x[45:75], y[45:75], 2)
p = np.poly1d(z)